Kalkulus
Assalamu’alaikum Wr. Wb.
Deskripsi MK:
Mata kuliah ini ditujukan kepada mahasiswa untuk mempelajari konsep-konsep mengenai limit fungsi, kenkontinuan turunan, integral tentu dan integral tak tentu, definisi, sifat-sifat, teorema, dan penerapan dalam soal-soal. Adapun materi perkuliahan yang akan dipelajari meliputi: system bilangan real, definisi turunan, sifat-sifat turunan, turuan dan kekontinuan, definisi integral, sifat-sifat integral, dan rumus-rumus integral.
Komponen Perkuliahan
Komponen penilaian :
Komponen | Persentase |
Tugas/kuis | 25% |
Partisipasi kuliah | 10% |
UTS | 30% |
UAS | 35% |
Konversi penilaian:
Referensi:
Varberg, D. & Purcell, E.J. 2001. Kalkulus (terjemah I.N. Susila, dkk). Jilid 1 Edisi VII. Jakarta. Interaksa
Capaian pembelajaran:
- Mampu memahami bilangan real
- Mampu memahami fungsi dan penerapannya
- Mampu memehamai persamaan dan pertidaksamaan linear
- Mampu memahami turunan dan komponenenya
- Mampu memahami integral dan fungsi intergral
PERTEMUAN 1: SISTEM BILANGAN REAL
Topik yang dipelajari:
- Sistem bilangan Real
- Nilai mutlak
- Akar kuadrat
- Kuadrat
Definisi Himpunan Bilangan
Himpunan bilangan merupakan kumpulan dari bilangan-bilangan. Himpunan bilangan meliputi: himpunan bilangan Asli, himpunan bilangan Cacah, himpunan bilangan Bulat, himpunan bilangan Rasional, himpunan bilangan Irrasional (tak terukur), dan himpunan bilangan Real.
Cara Menyelesaikan Ketaksamaan
Menyelesaikan operasi-operasi tertentu pada ketaksamaan yaitu tanpa mengubah himpunannya, adapun untuk menyelesaikannya dapat menggunakan cara berikut:
- Menambahkan bilangan yang sama pada kedua ruas ketaksamaan.
- Mengalikan kedua ruas ketaksamaan dengan suatu bilangan positif
- Mengalikan kedua ruas dengan suatu bilangan negative, tetapi kemudian kita harus membalikkan arah tanda ketaksamaan.
Definisi Nilai Mutlak
Nilai mutlak suatu bilangan real dinyatakan dengan , didefinisikan sebagai
Kuis: NILAI 60 /100
Soal 1
2^-3 * 2^7
=2^4
Soal 2
(3x^2y^5.10xy^3) / 6x^2y^4
=30x^2y^8 / 6x^2y^4
Jawab: D
Soal 3
|x+2|<1
|x+2|<1
=x+2-2 < 1-2
=x < -1
=x+2 >-1
=x+2-2 > -1-2
=x > -3
Jawab: A
Soal 4
|2x-1|>2
=2x-1+1 > 2+1
=2x > 3
=x > 3/2
=2x-1 < -2
=2x-1+1 < -2+1
=2x < -1
=x < -1/2
Jawab: B
Soal 5
a. |-x| = x
b. |x|^2 = x^2
c. |xy| = |x||y|
b. |x|^2 = x^2
c. |xy| = |x||y|
d. |x-y| >= |x| = |y|
e. |x| <= |x - y| + |y|
f. √x^2 = x
Jawab: C
TOPIK 2: FUNGSI
Informasi:
Assalamu'alaikum Wr. Wb.
Teman-teman...
Karena topik untuk pertemuan 2 ternyata sangat banyak jika dibuat dalam video, jadi untuk topik fungsi dan operasi fungsi silahkan dipelajari pada minggu ini. Sedangkan topik fungsi trigonometri silahkan dipelajari minggu depan untuk pertemuan ke-3. Untuk kuis, silahkan dikerjakan jika sudah selesai mempelajari semua topik pada pertemuan ke-3. Yang artinya, teman-teman punya waktu 2 minggu untuk menyelesaikan kuis dan materi bisa terus diakses untuk dipelajari kembali.
Best Regards,
Wassalamu'alaikum Wr. Wb.
Topik yang dipelajari:
- Operasi pada fungsi
- Fungsi trigonometri
Definisi Fungsi
Sebuah fungsi adalah suatu aturan padanan yang menghubungkan setiap objek dalam satu himpunan, yang disebut daerah asal, dengan sebuah nilai tunggal dari suatu himpunan kedua. Himpunan nilai yang diperoleh secara demikian disebut daerah hasil.
Materi PDF: Fungsi dan Grafik Fungsi
Materi PDF: Operasi pada Fungsi
Materi PDF: Fungsi Trigonometri
Materi PDF: Fungsi
Video pembelajaran dapat diakses di link berikut ini!
Operasi fungsi
Fungsi Trigonometri
Kuis Pertemuan 2 Nilai 40/100
Soal 1
f(x) = 3x - sqrt(2)
Jawab: A
Soal 2
f(x) = 3x - sqrt(2)
Jawab: D
Soal 3
Jika g(x) = (x³-3x) / sqrt(2), maka ƒ (√2) =
=(sqrt(2)^3 - 3sqrt(2))/sqrt(2)
=
Jawab: D
Soal 6
a. 6x - 9
b. 6x + 1
c. 9 - 6x
d. 1 - 6x
Jawab: D
Soal 7
Jawab: D
Soal 8
Berapakah radian dari 600?
Soal 9
Jawab: D
Soal 10
Tentukan nilai dari sin 120 dan tentukan letak kuadrannya!
TOPIK 3: LIMIT
Kuis Pertemuan 3 Nilai 71,43/100
Soal 1
Jawab: B
Soal 2
b. f(a) = 3
c. Jawaban A dan B benar
d. Jawaban A dan B salah
Jawab: A
Soal 3
Jawab: D
soal 4
Dari grafik di atas, nilai dari f(-2) adalah 2.
Pilih satu:
a. Benar
b. Salah
Jawab: A
Soal 5
Jawab: B
Soal 6
Jawab: B
Soal 7
Jawab: B
TOPIK 4: KEKONTINUAN FUNGSI
Materi PDF: Kekontinuan Limit
Materi Video:
Kuis Pertemuan 4 Nilai 55,56/100
Soal 1
Maka nilai f(0) adalah tidak terdefinisi.
Pilih satu:
a. Benar
b. Salah
Jawab: A
Soal 2
Nilai dari f(2) adalah 8.
Pilih satu:
a. Benar
b. Salah
Jawab: A
Soal 3
Jawab: B
Soal 4
Jawab: A
Soal 5
Pilih satu:
a. Benar
b. Salah
Jawab: B
Soal 6
Jawab: A
soal 7
a. Tidak
b. Tidak terdefinisi
c. Iya
d. Terdefinisi
Jawab: A
Soal 8
Jawab: A
Soal 9
Berdasarkan fungsi dari soal 1-8, jika fungsi tersebut kontinu,
a. Karena mempunyai nilai pada masing-masing f(x) dan limitnya
b. Karena nilai f(x) = nilai limit
c. Jawaban A dan B benar
d. Karena limit kiri ≠ limit kanan
e. Karena nilai f(x) ≠ nilai limit
f. Jawaban D dan E benar
Jawab: F
Ujian Kompetensi 01 Nilai 57,14/100
Soal 1
Jawab: A
Soal 2
Soal 3
Soal 4
Jawab: C
Soal 5
Carilah domain dan range dari fungsi berikut ini!
a. Domain = (0, 2) dan [3, 4]
Range = (0, 3)
b. Domain = (0, 2) dan [3, 4)
Range = (0, 3)
c. Domain = [0, 2) dan (3, 4)
Range = (0, 3)
d. Domain = (0, 2] dan [3, 4)
Range = (0, 3)
Jawab: A
Soal 6
Perhatikan fungsi-fungsi di atas, apakah tersebut kontinu di x?
a. Kontinue di f(x)
b. Tidak Kontinu di x
c. Kontinu di x
Jawab: B
Soal 7
Jawab: D
TOPIK 5: TURUNAN
Materi PDF: Turunan
Latihan Soal: Latihan Soal Turunan
Kuis Pertemuan 5 Nilai 50/100
Soal 1
Pilih satu:
a. Benar
b. Salah
Jawab: A
Soal 2
Jawab: A
soal 3
Pilih satu:
a. Benar
b. Salah
Jawab: B
Soal 4
Jawab: B
Soal 5
Jawab: A
Soal 6
Jawab: B
TOPIK 6: ATURAN RANTAI DAN NOTASI LEIBNIZ
Materi PDF: 7.1 ATURAN RANTAI DAN NOTASI LEIBNIZ
Latihan Soal: Latihan Soal
Kuis Pertemuan 6 Nilai 60/100
Soal 1
Jawab: A
Soal 2
Jawab: A
Soal 3
Jawab: B
Soal 4
Jawab: B
Soal 5
Jawab: A
TOPIK 7: TURUNAN TINGKAT TINGGI
Video Pembelajaran Turunan
Note:
Kesalahan pengucapan
k = konstanta bukan skalar
Kuis Pertemuan 7 Nilai 20/100
Soal 1
Soal 2
Jawab: B
Soal 3
Jawab: A
Soal 4
Jawab C
Soal 5
Jawab: D
TOPIK 8: DIFERENSIAL DAN HAMPIRAN
UJIAN TENGAH SEMESTER
Jawab:
Untuk menentukan nilai dari ekspresi (3x^2y^5.10xy^3) / (6x^2y^4) saat x = -10 dan y = 7, kita cukup mengganti x dan y dengan nilai yang diberikan dan melakukan perhitungan.
Mengganti x = -10 dan y = 7 ke dalam ekspresi:
(3(-10)^2(7)^5.10(-10)(7)^3) / (6(-10)^2(7)^4)
Sekarang, kita dapat menyelesaikan perhitungan ini:
(3(100)(16807)(-10)(343)) / (6(100)(2401))
Simplifikasi:
(-1808100) / (14406)
Hasilnya adalah -125.72854 (pembulatan ke lima angka di belakang koma).
Jadi, ketika x = -10 dan y = 7, nilai ekspresi tersebut adalah -125.72854.
Soal 2
Jika 2log 5 = p, maka tentukan nilai 2log 40 !
Jawab:
Jika 2log 5 = p, kita dapat menggunakan sifat logaritma untuk menentukan nilai dari 2log 40.
Perhatikan bahwa 40 dapat diurai menjadi faktor-faktor prima, yaitu 2^3 * 5^1. Kita dapat menulis 40 sebagai 2^3 * 5^1.
Menggunakan sifat logaritma, kita dapat mengurai logaritma dari produk menjadi penjumlahan logaritma individu:
log (40) = log (2^3 * 5^1)
= log (2^3) + log (5^1)
= 3 log (2) + log (5)
Kemudian, kita diketahui bahwa 2log 5 = p. Maka, kita bisa menyusun ulang persamaan ini untuk mendapatkan log 5 dalam bentuk p:
2log 5 = p
log 5^2 = p
log 25 = p
Sekarang, kita dapat menggantikan log 25 dengan p dalam persamaan sebelumnya:
log (40) = 3 log (2) + log (5)
= 3 log (2) + log 25
= 3 log (2) + p
Jadi, nilai dari 2log 40 adalah 3 log (2) + p.
Soal 3
Diketahui g(x) = sqrt(3x - 5) dan f(x) = 4x^3 + 1, tentukan gof(x)!
Jawab:
Untuk menentukan g o f(x) (g dari f(x)), kita perlu menggantikan setiap kemunculan x dalam fungsi g dengan f(x). Dalam hal ini, f(x) = 4x^3 + 1.
Sehingga, kita dapat menggantikan x dalam fungsi g(x) dengan f(x):
g o f(x) = g(f(x))
= sqrt(3f(x) - 5)
= sqrt(3(4x^3 + 1) - 5)
= sqrt(12x^3 + 3 - 5)
= sqrt(12x^3 - 2)
Jadi, g o f(x) = sqrt(12x^3 - 2).
Soal 4
Dodi, Rangga, Dias, Dimas, dan Laras sedang memainkan permainan ular tangga. Himpunan semesta pada dadu adalah A yang
beranggotakan 1,2,3,4,5,6. Masing-masing pemain diperbolehkan untuk melemparkan dadu sebanyak 2 kali dalam satu permainan. Saat
melemparkan dadu Laras mendapatkan 6 berturut, Dimas mendapatkan 2 dan 5, Dias mendapatkan 1 dan 2, Rangga mendapatkan 3 dan 6,
sedangkan Dodi mendapatkan 3 dan 5. Jika himpunan A adalah pemain yang mendapatkan angka 2 dan 6, sedangkan himpunan C adalah
pemain yang mendapatkan angka 4, jelaskan himpunan apa saja yang dihasilkan dan gambarlah diagram Venn-nya!
Jawab:
Berdasarkan informasi yang diberikan, kita dapat mengidentifikasi himpunan-himpunan yang ada dalam permainan ini:
Himpunan A: Pemain yang mendapatkan angka 2 dan 6 (Laras dan Rangga)
Himpunan B: Pemain yang mendapatkan angka 4 (Tidak ada pemain yang mendapatkan angka 4)
Himpunan C: Pemain yang mendapatkan angka 2 atau 5 (Dimas, Dias, dan Dodi)
Sekarang, kita dapat menggambarkan diagram Venn untuk memvisualisasikan himpunan-himpunan ini:
css
Copy code
A: {Laras, Rangga}
/
A∩C: {}
\
C: {Dimas, Dias, Dodi}
Dalam diagram Venn ini, A mewakili pemain yang mendapatkan angka 2 dan 6 (yaitu Laras dan Rangga). Himpunan A∩C (himpunan irisan antara A dan C) tidak memiliki anggota karena tidak ada pemain yang mendapatkan angka 2 atau 6 dan angka 2 atau 5 secara bersamaan. Himpunan C mewakili pemain yang mendapatkan angka 2 atau 5 (yaitu Dimas, Dias, dan Dodi).
Namun, perlu diperhatikan bahwa tidak ada pemain yang mendapatkan angka 4, sehingga himpunan B tidak memiliki anggota dalam konteks ini.
Dengan demikian, himpunan-himpunan yang dihasilkan adalah:
Himpunan A: {Laras, Rangga}
Himpunan B: {}
Himpunan C: {Dimas, Dias, Dodi}
Soal 5
Jika R(s) = s/(s^2 - 1), maka dy/dx adalah...
Jawab:
Untuk menentukan dy/dx dari persamaan R(s) = s/(s^2 - 1), kita harus menganggap bahwa s adalah fungsi dari x, yaitu s = s(x).
Dalam kasus ini, kita perlu menerapkan aturan rantai (chain rule) untuk mendapatkan dy/dx. Aturan rantai menyatakan bahwa jika y adalah fungsi dari u dan u adalah fungsi dari x, maka dy/dx dapat dinyatakan sebagai (dy/du) * (du/dx).
Mari kita lakukan penurunan terhadap persamaan R(s) terlebih dahulu:
R(s) = s/(s^2 - 1)
Kita dapat menulisnya ulang sebagai:
y = s/(s^2 - 1)
Sekarang, kita perlu mengekspresikan y sebagai fungsi dari x. Dalam hal ini, kita perlu mengubah s menjadi fungsi dari x, yaitu s = s(x).
Jika kita membedakan persamaan terhadap x, kita harus menggunakan aturan rantai untuk mendapatkan dy/dx:
dy/dx = (dy/ds) * (ds/dx)
Pertama-tama, kita hitung dy/ds dari persamaan y = s/(s^2 - 1). Untuk melakukan ini, kita perlu menggunakan aturan turunan bagi:
dy/ds = [(ds/ds) * (s^2 - 1) - s * (d(s^2 - 1)/ds)] / (s^2 - 1)^2
= (s^2 - 1 - s * (2s)) / (s^2 - 1)^2
= (s^2 - 1 - 2s^2) / (s^2 - 1)^2
= (-s^2 - 1) / (s^2 - 1)^2
Selanjutnya, kita perlu menghitung ds/dx. Karena s = s(x), maka ds/dx adalah turunan parsial dari s terhadap x.
Setelah mendapatkan dy/ds dan ds/dx, kita dapat menggabungkannya untuk mendapatkan dy/dx:
dy/dx = (dy/ds) * (ds/dx)
= (-s^2 - 1) / (s^2 - 1)^2 * ds/dx
Namun, kita perlu mengetahui persamaan s(x) yang menghubungkan s dengan x untuk menghitung ds/dx secara spesifik. Jika kita memiliki persamaan s(x), kita dapat menggantikan ds/dx dengan turunan dari persamaan tersebut.
Dalam kasus ini, tanpa informasi tambahan mengenai persamaan s(x), tidak mungkin memberikan nilai yang pasti untuk dy/dx. Oleh karena itu, kita tidak dapat menentukan dy/dx secara spesifik dengan informasi yang telah diberikan.










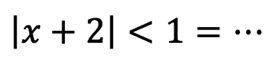
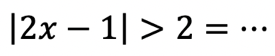
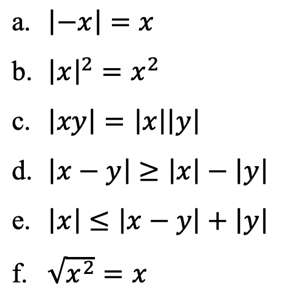





























































































Komentar
Posting Komentar
Semoga bermanfaat dunia dan akhirat